石英晶體諧振器各級溫度系數的確定
很多生產廠家采購石英晶體諧振器時,對工作溫度都有要求,因為怕產品會容易發熱或者爆炸。常規的貼片晶振工作溫度范圍是-30℃~+85℃,-40℃~+85℃;高要求的例如車規級的,一般是-40℃~+105℃,-40℃~+125℃甚至是-40℃~+150℃都有,根據產品的性能和要求選擇。工作溫度與頻率,精度,負載電容,封裝尺寸并稱為晶振五大參數。
圖3.2.3表示AT切型頻率溫度特性的典型測量結果。圖中,T0為某一參考溫度,Tm和Tn為極大點和極小點的溫度,(△f/f0)m和(△f/f0)n分別為極大點和極小點的相對頻率,a0、b0、c0與這些量的關系為

這說明,只要測得AT切型晶體元件的(△f/f0)m、(△f/f0)n和Tm、Tn、T0等的數值,然后代入上式(3.2.6),即可得到所需的a0、b0、c0的數值。
除了用頻率溫度特性來描寫貼片晶振元件的溫度特性外,還經常用頻率溫度系數
來表示晶體元件的溫度特性,頻率溫度系數的數學表示式為
TF=1/f0(∂f/∂T) (3.2.7)
式中,TF為頻率溫度系數,1/f0(∂f/∂T)為頻率隨溫度的相對變化率。應該注意
TF和a0、b0、c0的之間的區別,TF為任意溫度T時的頻率溫度系數,而a0、b0
C0為參考溫度T0時的一級、二級、三級溫度系數,即:0

將式(3.2.4)代入(3.2.7) 可得:
TF=a0+2b0(T-T0)+3c0(T-T0)2; (3.2.9)
由式(3.2.9)可以看出:
(1)晶體元件的頻率溫度系數TF與一級、二級、三級系數有關;
(2)晶體元件的頻率溫度系數TF是溫度的函數,因此頻率溫度系數是在某一溫度時的頻率溫度系數;
(3)頻率溫度系數的大小,反應了石英晶體元件的溫度穩定性;
(4)當T=T0時,則TF=a0,這表明只有在a0=0的條件下,才存在零溫度系數,所以,a0=0的切型稱為零溫度系數切型。
下表給出了各級頻率溫度系數的數值,以及這些系數隨切角的變化率,將表中有關數據代入下式,即可作出所需的頻率溫度特性曲線。
表3.2.1AT切各級頻率溫度系數的及其隨切角的變化


例如,將表中人造水晶n=1,θ=35°16’的系數代入式(3.2.10)可得:
求基準角(即φ1=φ0)時的頻率溫度特性方程為:

對上式進行二次微分,且(∂^2(?f/f))/(∂T^2 )=0,求拐點溫度:

∴T=8.35+20=28.35℃,即為拐點溫度。
【例】求歸一化頻率溫度度特性曲線上+3’時的向下翻轉點Tm和向上翻轉點Tn,φ1=3’=0.05°,對式(3.2.11)進行一次微分,(∂(?f/f))/∂T=0,則:


貝赫曼(R. Bechmann)總結了多方面試驗結果,得到無源晶振元件的頻率溫度特性曲線族的方程如下:

對式(3.2.12)進行一次微分,且φ1=φ0 (即基準角)得:

再進行二次微分得:

則(T-Ti)=-0.078/0.0657=-1.19℃,當Ti=27℃時,則T=27-1.19=25.89℃,即為拐點溫度。
【例】求歸一化頻率溫度特性曲線上+3′時的向下翻轉點Tm和向上翻轉點Tn
(55頁圖)φ1=3’,對式(3.2.12)進行一次微分,且(∂(?f/f))/∂T=0,則:
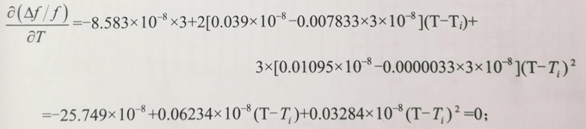
當Ti=25.89℃時:
Tn=x1+25.89=52.958℃。
Tm=x2+25.89=-3.076℃。
上述所計算的結果與實際生產的晶振元件的測量結果比較接近。
相關技術支持
- FCD-Tech石英晶體F2520A-30-50-K-30-F-34.000MHz術語和定義理論
- ECS許多應用需要石英振蕩器ECS-100AX-110.5和其他定時解決方案
- Abracon超小型ABS05-32.768KHZ-T音叉晶體專為節能MCU而優化
- Bliley壓控晶振BVCS5-24.000MHZMDN-ABCBT如何工作?
- Microchip用于嵌入式系統的新型PIC18F06Q20微控制器(MCU)
- Golledge下一代GSRFTA0942A頻率控制5G網絡的解決方案
- CTS最新推出的OCXO完美應用于各個領域
- 遙遙領先的Harmony Electronics Corp.用水晶增強安全駕駛
- 了解遙遙領先的SIWARD希華晶體振蕩器
- 領先全球Skyworks晶振為下一代Wi-Fi 6/6E設備提供前所未有的能效


 手機版
手機版














